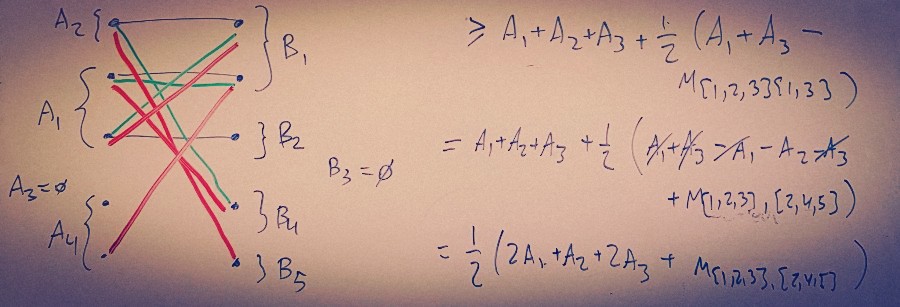Of particular relevance is conceptually-simple online algorithms for decision making problems in which irrevocable decisions are needed to be made in the face of input uncertainty. The focus on this project is on conceptually-simple algorithms for various computational problems such as bipartite matching problem and dual bin packing.
Bipartite matching has enormous implications in online advertising along with many other decision making problems. The bipartite matching problem is specified by matching elements of two disjoint sets to each other (for example, matching buyers to sellers) when there are some constraints on whether two elements can be matched with each other at all. Although the current bipartite matching algorithms are efficient when the number of buyers and sellers is small, they fall short in two ways. First, they are conceptually hard to understand for programmers, users, and even policy makers. Second, they become relatively inefficient when the size of the problem is large (e.g., when millions of buyers needs to be matched with millions of sellers). Our recent research has tackled these two problems by proposing an iterative conceptually-simple algorithm, which can handle large-scale bipartite decision making.
We also proposed and studied a simple polynomial-time approximation scheme (PTAS) for the online dual bin packing problem and prove its advice complexity.